이번 포스팅은 이전 포스팅인 1의 보수 편을 참고해주시길 바랍니다.
1의 보수 방식
1의 보수 방식 ① 일반적으로 컴퓨터는 2진법을 사용하므로 컴퓨터가 사용할 수 있는 보수 방식에는 1의 보수 방식과 2의 보수 방식이 있다. ② 1의 보수 방식은 'X = A + B' 에서 기준치 X를 11111...1
hemahero.tistory.com
2의 보수 방식 그리고 1의 보수 방식과의 관계(2's complement and the relation with 1's complement)
① 2의 보수 방식은 'X = A + B' 에서 기준치 X를 0000....0000(n비트만큼 존재)으로 잡은 것이다.
㉠ 즉, 4비트를 기준으로 한다면, 기준값은 0000이 된다.
② 2의 보수 방식으로 보수 처리하는 방법은 1의 보수로 만든 후, +1을 해주면 된다.
㉠ +1을 해주는 이유에 대해서는 아래 그림을 참고하자.

ⓐ 양수는 아무런 문제가 없다. 그런데, 하필이면 1의 보수 방식에 0000..00 = 1111..11인 0이 존재한다. 따라서 1111..11을 0이 아닌 -1로 만들어주는 과정에서 모든 음수를 한 칸 씩 평행이동하는 과정에서 +1이 더해지는 것이다.
ⓑ 예를 들어 0000(0)을 2의 보수처리하면, 1111에 +1을 해줘서 1 0000이 된다. 최상위 비트에서 캐리가 발생했기 때문에 캐리된 수인 1은 무시된다. 결국 0000(0)이 된다.
ⓒ 두 번째 예시로, 0001을 2의 보수처리하면, 1110에 +1을 해줘서 1111(-1)이 된다. 0001과 1111을 더하면 1 0000 = 0000이 된다. 기준값이 되기 때문에 옳게 2의 보수처리했음을 알 수 있다.
2의 보수와 음수
① 보수와 음수는 무슨 관계가 있는 것일까?
㉠ 다음 그림을 보자.

② 보수처리한 수를 0에 더하면, 보수처리하기 전의 수의 음수와 같다.
③ 부호화 절댓값과 1의 보수방식과는 달리 -0이 없다.
④ 다음 표는 4비트일 때 2의 보수방식으로 나타낼 수 있는 모든 경우의 수를 나타낸 것이다.
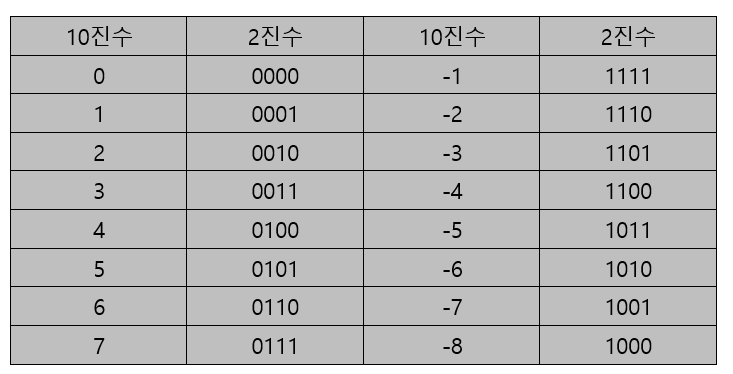
⑤ 다음 표는 음수 계산 중 나올 수 있는 상황을 정리한 것이다.


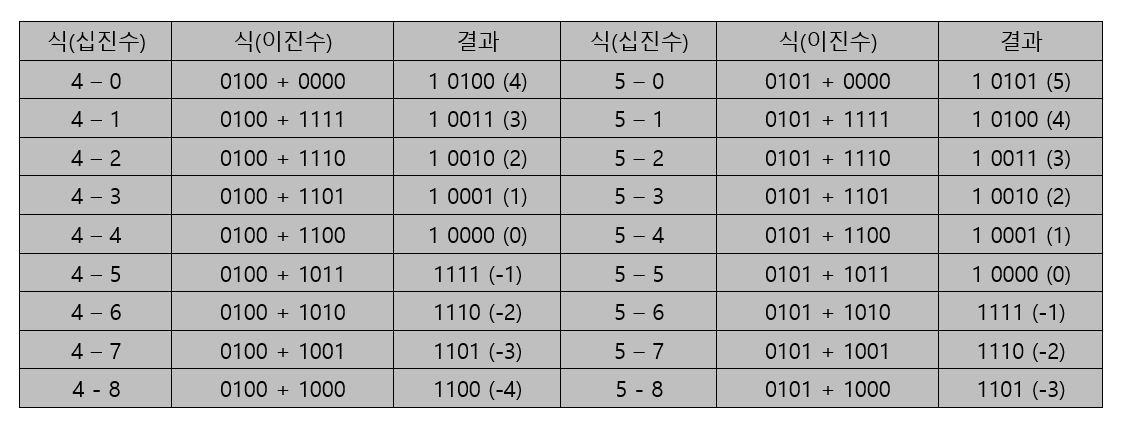
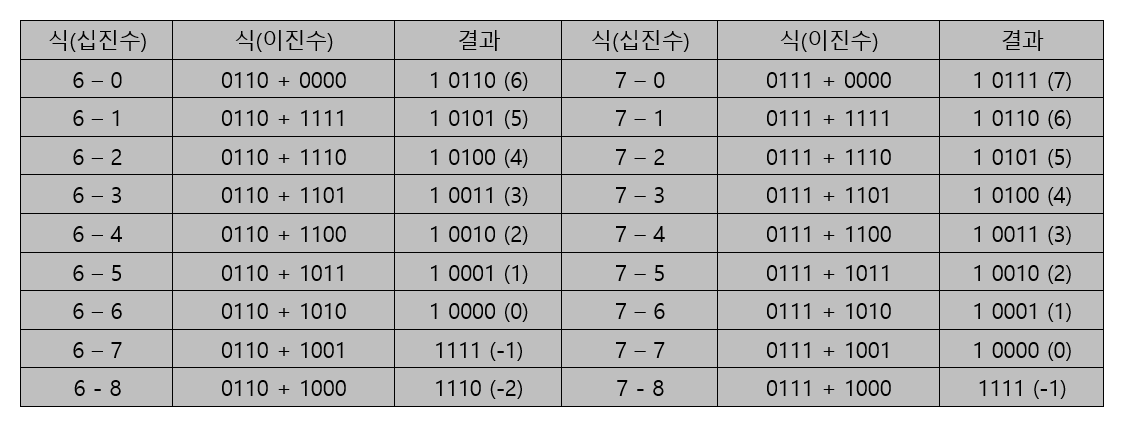


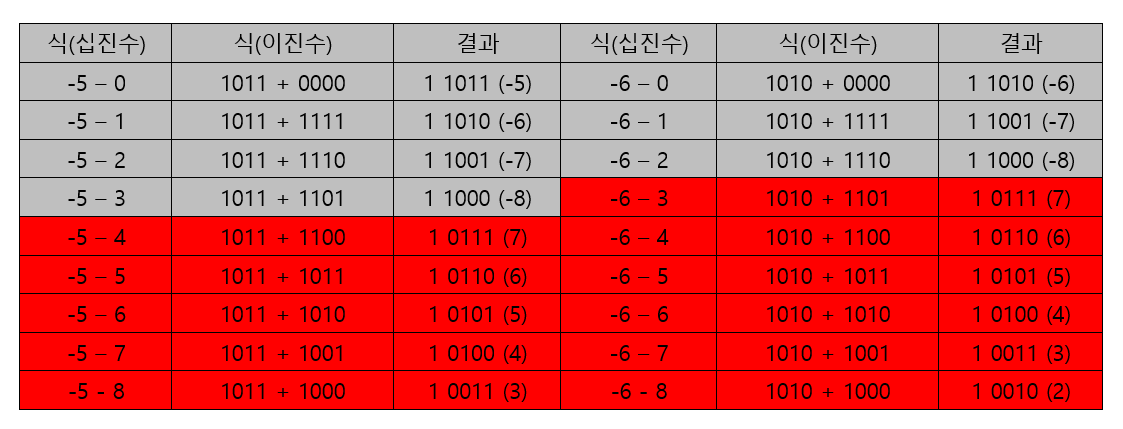

㉠ 위의 표들의 계산 결과를 봤을 때 회색, 빨간색으로 나뉜다.
㉡ 회색으로 색칠된 부분은 계산을 수행했을 때 정상인 부분이다.
ⓐ 아래 그림을 보면 십진수로 계산한 것과 이진수로 계산한 것이 같음을 알 수 있다.
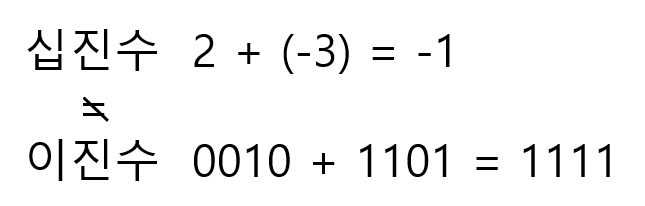
㉢ 빨간색으로 색칠된 부분은 4비트로 나타낼 수 있는 수의 범위를 벗어난 부분이다.
ⓐ 4비트로 나타낼 수 있는 수의 범위는 -8~7이다. 따라서 7 초과 또는 -8 미만이 이 경우에 해당한다.
ⓑ 아래 그림을 보면 십진수로 계산한 것이 4비트로 나타낼 수 있는 범위를 초과했음을 알 수 있다.

ⓒ 4비트일 때는 이 오류를 해결할 방법이 없다. 하지만 이를 일반화한다면 이 문제가 해결된다.
⑥ 이진수의 2의 보수 계산을 일반화하면 아래와 같다.
㉠ 기준치는 0000...000이라고 가정하며, 4비트까지만 나타낸다고 해보자.
ⓐ 4비트일 때는 -8~7까지만 나타낼 수 있다고 제한했으나, 현재는 나타낼 수 있는 수의 범위 제한이 없다.
ⓑ 하지만 일반적인 상황에서 굳이 모든 비트를 표시하지 않더라도 적당한 수의 비트를 제외한 비트들을 생략해서 표시하면 된다.
ⓒ 따라서 4비트에서는 4비트를 초과한 이진값들을 생략하기 때문에 하나의 값이 2개의 값을 갖는 것처럼 보인다.
ⓓ 예를 들어 -13와 3을 들 수 있다.
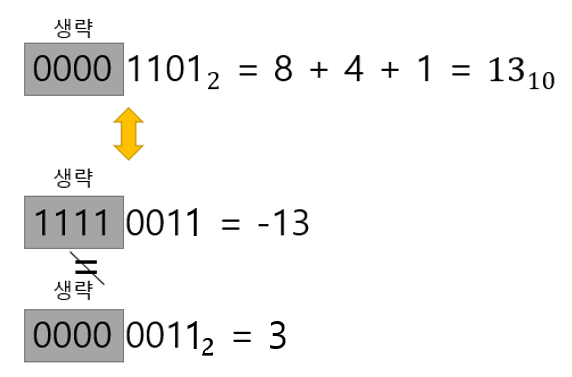
㉡ 표의 계산에서 문제가 생기는 상황들의 공통점은 최상위 비트에서 캐리가 발생한다는 것이다.
ⓐ 따라서 최상위 비트에서 캐리가 발생하는 것과 발생하지 않는 경우로 나눌 수 있다.
ⓑ 일반화시킨 캐리가 발생하는 경우는 다음과 같다.
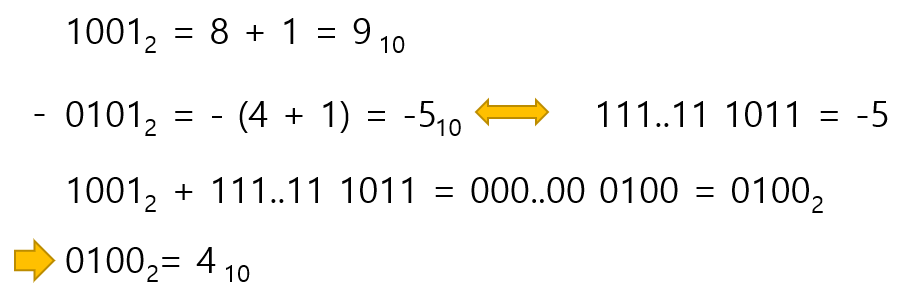
ⓒ 일반화시킨 캐리가 발생하지 않는 경우는 다음과 같다.

⑦ 부호화 절댓값과는 다르게 a - b를 a + (-b)로 계산하기 때문에 가산기(덧셈기)로만 계산하는 것이 가능하다.
⑧ 2의 보수 방식으로 된 수열의 값이 무엇인지 빨리 알 수 있는 신기한 방법이 있다. 1의 보수 방식에서 구한 것과 유사하다.
㉠ 예를 들어 1010은 -8 + 2 = -6이다.
㉡ 예를 들어 1111 0001은 -128 + 64 + 32 + 1 = -31이다.
㉢ 참고로 이진수를 십진수로 변환할 때, 변환과정은 아래과 같다.

이진수와 범위
① 이진수를 표현할 수 있는 범위는 무한한 것이 아니다. 쓸데없이 많은 범위를 실제로 모두 쓴다는 것이 불가능할 뿐더러, 경제적으로 낭비이기 때문이다.
② 부호화 절댓값과 1의 보수 방식은 나타낼 수 있는 값의 범위가 같다. 2의 보수 방식은 부호화 절댓값과 1의 보수 방식보다 아래로 1개 더 많다.
③ 다음 그림은 이진수가 나타낼 수 있는 경우의 수이다.

④ 다음 그림은 부호화 절댓값, 1의 보수 방식, 2의 보수 방식이 가질 수 있는 범위를 일반화시킨 것이다.

㉠ 부호화 절댓값의 경우, 양수와 음수가 절댓값은 같고, 최상위 비트만 다르므로, 둘다 2n-1의 경우의 수를 가지기 때문에 2 X 2n-1=2n이다.
㉡ 1의 보수 방식의 경우, 1의 보수는 양수의 1을 0으로, 0을 1로 바꾸는 것이기 때문에 양수와 음수의 각각 대응된다. 양수의 경우의 수는 2n-1이다. 음수가 양수에 대응되므로, 2 X 2n-1=2n이다.
㉢ 2의 보수 방식의 경우, 1의 보수 방식에서 -0을 제거하고, 음수 쪽으로 한 칸씩 평행이동했기 때문에, -0 대신 음수가 있다.
오버플로와 언더플로
① 오버플로라는 말의 의미는 위로 넘쳐 흐른 것이다. 이와 대조되는 용어로 언더플로가 있다. 언더플로는 아래로 넘쳐 흐른 것이다.
② 넘쳤다는 말은 즉슨, 원래는 한계가 있었다는 것이다. 표시하고자 하는 범위를 넘어갔기 때문에 다시 처음으로 넘어가는 것이다.
③ 오버플로를 이해하기 위해선 아래 사진을 먼저 이해하는 것이 필요하다.

㉠ 2진수를 위의 사진과 같이 회전판이라고 생각해보자.
㉡ 예를 들어 0001(1)+0010(2) = 0011(3)를 표현하려고 한다. 0000에서 화살표 방향으로 1칸을 움직여주고, 2칸을 움직여주면 0011(3)이 된다.
㉢ 4비트에서 2의 보수 방식으로는 -8~7까지 표현할 수 있다. 그렇다면, 범위를 넘어가면 어떻게 될까?
ⓐ 예를 들어 0110(6) + 0011(3)을 계산해보자. 0000에서 화살표 방향으로 6칸을 움직여주고, 3칸을 움직여주면 1001(-7)이 된다. 원래라면 9가 나와야하지만, 전혀 다른 결과가 나왔다. 이것을 오버플로(overflow)라고 한다.
ⓑ 예를 들어 1100(-4) + 1011(- 5)를 계산해보자. 0000에서 화살표 반대 방향으로 4칸 움직여주고, 5칸을 움직여주면 0111(7)이 된다. 원래라면 -9가 나와야하지만, 전혀 다른 결과가 나왔다. 이것을 언더플로(underflow)라고 한다.
㉣ 이것의 원리가 무엇인지 봐보자.
ⓐ 첫 번쨰 예시였던 0110(6) + 0011(3)를 식으로 계산해보자. 아래 그림을 참고하자.

ⓑ 첫 번쨰 예시였던 1100(-4) + 1011(- 5)를 식으로 계산해보자. 아래 그림을 참고하자.

④ 오버플로와 언더플로는 한 눈에는 다른 계산과 구별이 가지 않는다. 따라서 오버플로와 언더플로를 방지하려면, 둘의 특성을 알아야 한다.
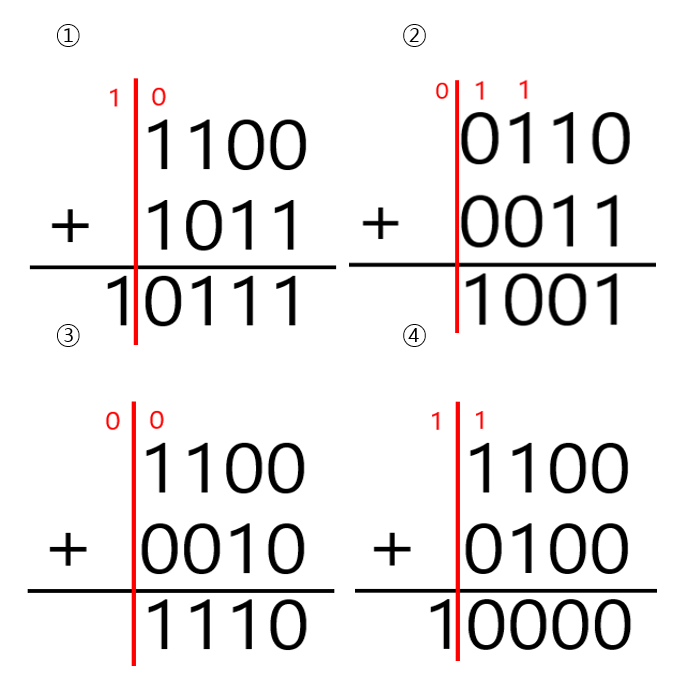
㉠ ①~④번 중에 오버플로 또는 언더플로인 것은 ①번과 ②번이다.
㉡ 최상위 비트와 그 다음 5번째 비트의 캐리를 보면 알 수 있다.
㉢ 캐리가 01이면 오버플로, 10이면 언더플로이며, 11 또는 00이면 정상이다.
'All about Computer > 이론' 카테고리의 다른 글
| 깊은 복사와 얕은 복사 (0) | 2022.07.09 |
|---|---|
| Call by Reference와 Call by Value (0) | 2021.08.21 |
| 이진수의 음수표현(1의 보수 방식) (0) | 2021.01.11 |
| 9의 보수 방식, 10의 보수 방식 (0) | 2021.01.11 |
| 이진수의 음수 표현(부호화 절댓값의 덧셈과 뺄셈) (0) | 2021.01.11 |

