1. 이진수의 음수 표현
① 십진수에서는 음수를 표현하고 싶으면 -(마이너스 기호)를 사용하면 되지만, 이진수에서는 특이한 방식으로 음수를 표현한다.
② 보수를 이용해 음수를 나타내는 방법은 무려 4가지나 있는데, 부호화 절댓값(sign and mignitude), 1의 보수 방식(one's complement), 2의 보수 방식(two's complement), 그리고 상쇄 이진수(offset binary)가 있다.
㉠ 그러나 실제로는 2의 보수 방식을 주로 사용하는데, 이유는 편리함과 경제적 효율성 때문이다.
③ 비트의 크기가 4인 경우를 생각해보자. 한 비트는 두 가지 수 0과 1을 표현할 수 있으므로, 총 16가지의 경우의 수를 가지고 있다.

㉠ 따라서 아래와 같은 16가지의 경우의 수가 만들어지게 된다.
| 10진수 | 2진수 | 10진수 | 2진수 |
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | 10 | 1010 |
| 3 | 0011 | 11 | 1011 |
| 4 | 0100 | 12 | 1100 |
| 5 | 0101 | 13 | 1101 |
| 6 | 0110 | 14 | 1110 |
| 7 | 0111 | 15 | 1111 |
2. 부호비트
① 부호비트는 음수를 나타내기 위해서 만들어졌다.
② 제일 왼쪽에 있는 최상위 비트가 부호를 나타내도록 설정하는 것이 부호비트이다.

③ 1의 보수, 2의 보수, 부호화 절댓값 방식에서 모두 통용되는 방식으로, 부호비트가 0이면 양수 혹은 양의 0을, 1이면 음수 혹은 음의 0을 나탄낸다.
㉠ 이 때, 최상위 비트는 제일 왼쪽으로 위치는 같지만, 기억소자를 몇 비트로 설정할 지에 따라 나타낼 수 있는 값의 범위가 달라진다. 여기에서는 4bit를 가정하고 설명하겠다.
3. 부호화 절댓값
① 말 그대로 어떤 '값'이 부호를 갖게 되었다는 것이다. 가장 직관적으로 음수를 표현하는 방식이다.
② 부호비트를 제외하고, 나머지 비트는 절댓값이 같으면 양의 2진수를 표현하는 방법과 같다.
| 10진수 | 2진수 | 10진수 | 2진수 |
| 0 | 0000 | -0 | 1000 |
| 1 | 0001 | -1 | 1001 |
| 2 | 0010 | -2 | 1010 |
| 3 | 0011 | -3 | 1011 |
| 4 | 0100 | -4 | 1100 |
| 5 | 0101 | -5 | 1101 |
| 6 | 0110 | -6 | 1110 |
| 7 | 0111 | -7 | 1111 |
③ 부호화 절댓값 방식은 정말 직관적이기 때문에 부동소수점을 표현할 때 주로 사용된다.
④ 일단 부호비트와 절댓값을 따로 계산해줘야하는 단점이 있다.
⑤ 부호화 절댓값 방식을 사용하면 특정상황에서 오류가 생기는 단점이 있다. 아래에서 설명하겠다.
⑥ 부호화 절댓값에는 0이 두개 존재한다.
4. 부호화 절댓값의 덧셈과 뺄셈
① 부호가 같은 부호화 절댓값의 덧셈은 일반 십진수 연산과 동일하다.
㉠ 3 + 2 = 5를 계산하면 아래와 같다.

ⓐ 부호비트의 계산 방법은 절댓값의 계산 방법과는 다른데, A+B=C에서 A와 B가 양수이면 C도 양수여야 하므로 C의 부호비트는 0이어야 한다.
㉡ -3 -2 = -5를 계산하면 아래와 같다.
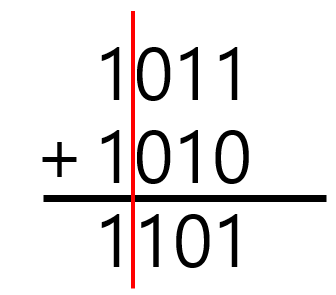
ⓐ 부호비트의 계산 방법은 절댓값의 계산 방법과는 다른데, A+B=C에서 A와 B가 음수이면 C도 음수여야 하므로 C의 부호비트는 1이어야 한다.
② 이진수의 뺄셈은 덧셈을 모방한다. 부호비트가 다른 덧셈은 이 경우에 해당한다.
㉠ A의 절댓값이 B의 절댓값보다 큰 경우는 A - B = A + (-B)와 같이 계산하다.
ⓐ 3 - 2 = 1을 3 + (-2)로 계산하면 어떻게 될까?
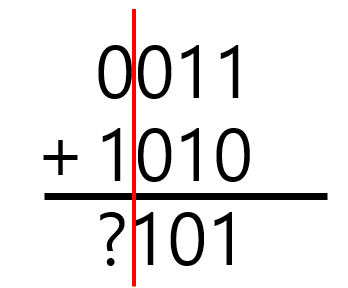
(a) 부호가 다른 부호비트는 가산기(덧셈기)로는 구할 수 없다. 아래와 같이 감산기(뺄셈기)를 사용해야 한다.

(b) 절댓값끼리 먼저 계산하면 011 - 010 = 001이다. 부호비트의 계산은 0 - 1이 되는데, -1은 음수에 마이너스 부호를 붙인 것이므로 양수인 0과 같다. 따라서 0 - 1 = 0 - (-0) = 0 + 0= 0이 되므로 0001이 된다.
ⓑ -3 + 2 = -1를 계산하면 어떻게 될까?

(a) 부호가 다른 부호비트는 가산기(덧셈기)로는 구할 수 없다. 아래와 같이 감산기(뺄셈기)를 사용해야 한다.

(b) 절댓값끼리 먼저 계산하면 011 - 010 = 001이다. 부호비트의 계산은 1 - 0이 되는데, -0은 양수에 마이너스 부호를 붙인 것으로 음수인 1과 같다. 따라서 1 - 0 = 1 - (-1) = 1 + 1= 1이 되므로 1001이 된다.
㉡ B의 절댓값이 A의 절댓값보다 큰 경우는 A - B = -B + A 와 같이 계산한다.
ⓐ -2+3=1을 계산하면 어떻게 될까?
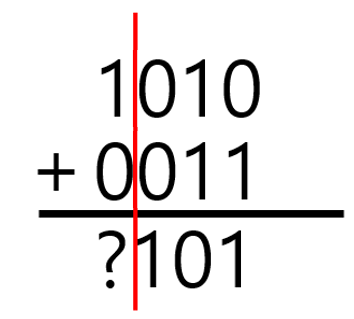
(a) -2 + 3 = 3 - 2과 같다.
(b) 부호가 다른 부호비트는 가산기(덧셈기)로는 구할 수 없다. 아래와 같이 감산기(뺄셈기)를 사용해야 한다. 단, 피감수가 감수보다 작으므로 둘의 순서를 바꿔서 계산해야 한다.

(c) 피감수와 감수의 순서를 바꾼 후 절댓값끼리 먼저 계산하면 011 - 010 = 001이다. 부호비트의 계산은 0 - 1이 되는데, -1은 음수에 마이너스 부호를 붙인 것이므로 양수인 0과 같다. 따라서 0 - 1 = 0 - (-0) = 0 + 0 = 0이 되므로 0001이 된다.
ⓑ 2 - 3 = -1을 계산하면 어떻게 될까?

(a) 2 - 3 = -3 + 2과 같다.
(b) 부호가 다른 부호비트는 가산기(덧셈기)로는 구할 수 없다. 아래와 같이 감산기(뺄셈기)를 사용해야 한다. 단, 피감수가 감수보다 작으므로 둘의 순서를 바꿔서 계산한 후에 마지막에 마이너스 부호를 붙여줘야 한다.

(c) 피감수와 감수의 순서를 바꾼 후 절댓값끼리 먼저 계산하면 011 - 010 = 001이다. 부호비트의 계산은 1 - 0이 되는데, -0은 양수에 마이너스 부호를 붙인 것이므로 음수인 1과 같다. 따라서 1 - 0 = 1 - (-1) = 1 + 1 = 1이 되므로 1001이 된다.
③ 부호화 절댓값을 사용할 때 고려해야하는 점은 2가지 있다.
㉠ 피연산자들의 부호비트가 같은가?
㉡ 피연산자들 중 절댓값이 큰 것은 어느 쪽인가?
④ 부호화 절댓값의 장점은 인간이 직관적으로 계산과정을 이해하기 쉽다는 것이다.
⑤ 부호화 절댓값의 단점은 가산기와 감산기를 따로 구현해야한다는 점, 0이 두 개나 존재하기 때문에 표현할 수 있는 수의 범위를 낭비 하게된다는 점, 부호비트 때문에 논리회로가 더 복잡해진다는 점이 있다.
'All about Computer > 이론' 카테고리의 다른 글
| Call by Reference와 Call by Value (0) | 2021.08.21 |
|---|---|
| 이진수의 음수표현(2의 보수, 오버 플로와 언더 플로) (0) | 2021.01.11 |
| 이진수의 음수표현(1의 보수 방식) (0) | 2021.01.11 |
| 9의 보수 방식, 10의 보수 방식 (0) | 2021.01.11 |
| 전처리 지시자 (0) | 2020.07.23 |


