9의 보수 방식과 10의 보수 방식의 개념
① 마이너스 기호(-)를 붙이지 않고 음수를 표현할 수 있는 방법이 존재한다.
㉠ 음수를 표현하기 전에 정수는 양의 정수, 0, 음의 정수로 이루어져있다는 것을 생각해보자.
ⓐ 0을 말 그대로 0으로 취급할 것인지, 아니면 양의 정수 혹은, 음의 정수의 일부로 포함시킬 건지를 고려해야한다.
② 음수를 나타내는 방법으로 보수를 이용하는 방법이 있다.
㉠ 보수는 아래의 네이버 사전에 명시된 것처럼, 각 자리의 숫자의 합이 어느 일정한 수가 되게 하는 수이다.

ⓐ A + B = C라면 C의 A에 대한 보수는 B이다.
㉡ 보수를 사용하는 근본적인 이유는 이진수의 뺄셈을 덧셈 과정으로 계산해 경제적 효율성을 높이기 위해서이다.
ⓐ 뺼셈과 덧셈을 두 가지의 구분되는 과정으로 만드는 것보다 한 가지의 과정으로 통일시키는 게 경제적으로 이익이다.
ⓑ 십진수로 보수를 표현할 때는 한 자리에 들어가는 경우의 수가 10가지나 되어 보수 계산의 이점을 충분히 활용할 수 없다.
ⓒ 반면, 이진수는 한 자리에 0 또는 1만 존재하기 때문에 보수 계산에서는 굉장히 유리하다.
ⓓ 그 이유는 이진수는 각 자릿수가 0과 1만으로 표현되므로, 양수 아니면 음수라는 개념과 0과 1이 수적으로 대응된다.
ⓔ 그러나 십진수는 각 자릿수가 0~9의 수로 표현되므로, 이진수만의 특성인 토글(toggle)이라는 개념과 일대일 대응하지 않기에 상대적으로 불리하다.
③ 십진수는 각 자리에 0부터 9까지의 수가 들어갈 수 있으므로 두 자릿수로 표현할 수 있는 경우의 수는 10x10 = 100 가지이다.
㉠ 십진수에서 보수를 나타내는 방식은 9의 보수 방식과 10의 보수 방식이 있다.
ⓐ 9의 보수 방식은 0을 양의 0과 음의 0으로 표현해 양의 정수와 음의 정수의 개수를 동일하게 하는 방식이다.
ⓑ 10의 보수 방식은 0을 0으로 취급하며, 음의 0이 존재하지 않기 때문에 음의 정수의 폭이 더 넓다.
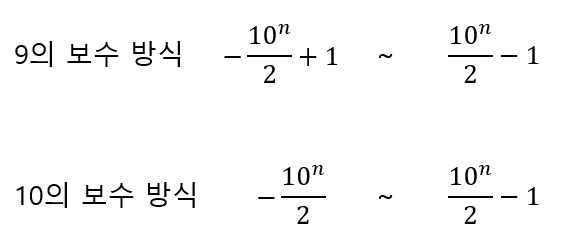
④ 특정 수와 그 수의 보수를 더했을 때 그 특정값은 0을 의미해야 한다.
㉠ 이 때 특정 값은 9의 보수 방식일 때는 10^n-1, 10의 보수 방식일 때는 10^n이다.(n은 자릿수이다.)

㉡ 9의 보수 방식일 때 10^n - 1은 음의 영(-0)을 의미하며, 양의 영과 보수 관계이다.
㉢ 10의 보수 방식에서는 10^n은 n+1 자리이기 때문에 오버플로가 일어나 0이 된다.
ⓐ 최대자릿수를 넘어간다면, 넘어간 자리의 숫자는 무시하는데 이를 오버플로(Overflow)되었다고 한다.
ⓑ 10의 보수 방식에서 음의 영 대신 음수를 한 개로 바꿨기 때문에 음수 마지막 수에 대응되는 보수 관계가 없다.

보수 방식을 이용한 뺄셈의 원리
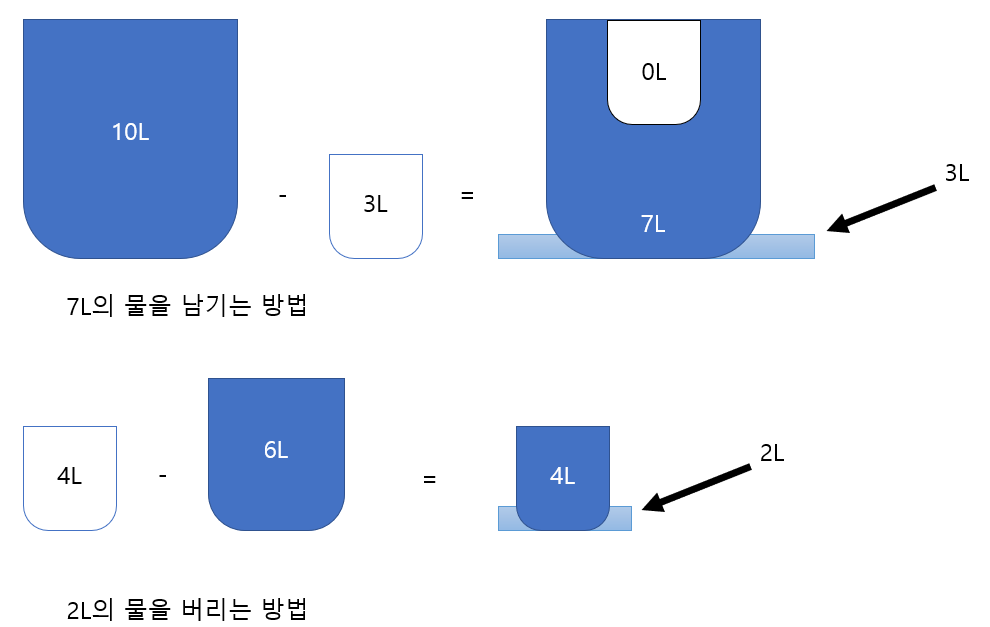
① 2개의 비커와 물을 이용해 뺄셈을 할 수 있다.
㉠ 큰 비커의 바닥에 흘린 물에 대한 보수는 큰 비커 안에 있는 물이다.
㉡ 큰 비커의 바닥에 흘린 물에 대한 보수는 작은 비커 안에 있는 물이다.
9의 보수 방식을 이용한 뺄셈의 계산 과정
① 우선 최대자릿수를 정해야 한다. 뺄셈에는 감수(빼는 수)와 피감수(빼지는 수)가 존재하므로, 둘을 비교해서 최대자릿수를 결정해야 한다.
㉠ 최대자릿수의 기준은 감수와 피감수의 자릿수에 있다. 즉, a - b라고 한다면, 최대자릿수는 a와 b 중 더 큰 수와 자릿수가 같다.
ⓐ 예를 들어 3 - 12의 경우 12가 더 크다. 12는 두 자리이므로, 최대자릿수는 2이다.
ⓑ 예를 들어 12 - 4의 경우 12가 더 크다. 12는 두 자리이므로, 최대자릿수는 2이다.
㉡ 기준 값은 최대자릿수와 같은 자릿수를 가진 수 중 최댓값이다.
㉢ 기준값은 10^n-1와 같다.(n은 최대자릿수)
ⓐ 3 - 12에서 최대자릿수는 2이다. 이 때, 최댓값은 99이다.
ⓑ 12 - 4에서 최대자릿수는 2이다. 이 때, 최댓값은 99이다.
② 두 번째로, 감수를 보수처리한다.
㉠ 12를 보수처리하면 87이 된다.
㉡ 4를 보수처리하면 95가 된다.
③ 피감수와 보수 처리된 감수를 더한다.
㉠ 3 + 87 = 90
㉡ 12 + 95 = 107
④ 만약 합이 최대자릿수를 넘어가지 않는다면, 합을 보수처리한 것의 음수값이 결과이다.
㉠ 90은 최대자릿수가 2이므로 이를 보수처리한 수는 9이고, 여기에 마이너스를 붙이면 -9가 된다.
⑤ 최대자릿수를 넘어간다면, 넘어간 자리의 숫자는 무시한다. 이를 오버플로되었다고 한다. 무시한 후, 결과값에 1을 더한다.
㉠ 107 은 최대자릿수를 넘어갔으므로, 오버플로가된 수는 무시하고, 7에 1을 더하면 8이 된다.


10의 보수 방식을 이용한 뺄셈의 계산 과정
① 우선 최대자릿수를 정해야 한다. 뺄셈에는 감수(빼는 수)와 피감수(빼지는 수)가 존재하므로, 둘을 비교해서 최대자릿수를 결정해야 한다.
㉠ 최대자릿수의 기준은 감수와 피감수의 자릿수에 있다. 즉, a - b라고 한다면, 최대자릿수는 a와 b 중 더 큰 수와 자릿수가 같다.
ⓐ 예를 들어 3 - 12의 경우 12가 더 크다. 12는 두 자리이므로, 최대자릿수는 2이다.
ⓑ 예를 들어 12 - 4의 경우 12가 더 크다. 12는 두 자리이므로, 최대자릿수는 2이다.
㉡ 기준 값은 최대자릿수와 같은 자릿수를 가진 수 중 최댓값이다.
㉢ 기준값은 10^n와 같다.(n은 최대자릿수)
ⓐ 3 - 12에서 최대자릿수는 2이다. 이 때, 최댓값은 100이다.
ⓑ 12 - 4에서 최대자릿수는 2이다. 이 때, 최댓값은 100이다.
② 두 번째로, 감수를 보수처리한다.
㉠ 12를 보수처리하면 88이 된다.
㉡ 4를 보수처리하면 96가 된다.
③ 피감수와 보수 처리된 감수를 더한다.
㉠ 3 + 88 = 91
㉡ 12 + 96 = 108
④ 만약 합이 최대자릿수를 넘어가지 않는다면, 합을 보수처리한 것의 음수값이 결과이다.
㉠ 91은 최대자릿수가 2이므로 이를 보수처리한 수는 9이고, 여기에 마이너스를 붙이면 -9가 된다.
⑤ 최대자릿수를 넘어간다면, 넘어간 자리의 숫자는 무시한다. 이를 오버플로되었다고 한다.
㉠ 108 은 최대자릿수를 넘어갔으므로, 오버플로가된 수는 무시하면 8이 된다.


⑥ 과정이 다소 복잡해 보인다. 뺄셈을 덧셈으로 계산하려 하는데, 보수를 구하는 과정에서 뺄셈을 하는 모순 현상이 생긴다.
㉠ 그러나 이는 십진수이고, 십진수에는 토글(toggle) 특성이 존재하지 않기 때문에 복잡해보인다.
㉡ 이진수의 경우 0과 1밖에 없기 때문에 토글 특성을 활용한다면 계산 결과를 간단하게 구할 수 있다.
㉢ 계산 과정이 복잡해 보이는 이유는 D가 어떤 수를 의미하는지 구하려고 하기 때문이다. D 상태는 어떤 수가 치환된 상태이므로 D 상태를 이용한다면 그리 복잡하지 않다.
'All about Computer > 이론' 카테고리의 다른 글
| Call by Reference와 Call by Value (0) | 2021.08.21 |
|---|---|
| 이진수의 음수표현(2의 보수, 오버 플로와 언더 플로) (0) | 2021.01.11 |
| 이진수의 음수표현(1의 보수 방식) (0) | 2021.01.11 |
| 이진수의 음수 표현(부호화 절댓값의 덧셈과 뺄셈) (0) | 2021.01.11 |
| 전처리 지시자 (0) | 2020.07.23 |


