※ 이 글은 chatGPT를 기반으로 작성한 글입니다.
① 마스터 정리(master theorem)는 복잡한 알고리즘(recursive algorithm)의 시간 복잡도를 구하기 위해 사용한다.
② 마스터 정리로 해결할 수 있는 알고리즘의 구조는 다음과 같은 꼴을 따른다.

㉠ a>=1, b>1 인 상수여야 한다.
㉡ f(n)이 점근적으로 양수 함수값을 가지는 함수여야 한다.
㉢ 설명의 편의를 위해 A항 B항이라고 칭하겠다.
③ A항은 상위 문제를 해결하기 위해 상위 문제(super problem)를 하위 문제(sub problems)로 분할하는 데 소요되는 시간 복잡도이다.
㉠ 상수 a는 재귀 함수가 호출하는 하위 재귀 함수의 숫자이다.
㉡ 하위 재귀 함수는 n/b의 크기로 분할된다.
㉢ 상위 문제의 1/2 사이즈인 2개의 하위 문제를 재귀적으로 호출한다.
| function rock(array) | |
| n = length(array) | |
| if n > 1 then | |
| rock(n/2) | |
| rock(n/2) | |
| end if | |
| end function |
ⓐ 재귀 관계식(Recurrence Relation)은 T(n) = 2T(n/2)이다.

ⓑ 시간 복잡도는 O(n)이다.

㉣ 상위 문제의 1/3 사이즈인 1개의 하위 문제를 재귀적으로 호출한다.
| function rock(array) | |
| n = length(array) | |
| if n > 1 then | |
| rock(n/3) | |
| end if | |
| end function |
ⓐ 재귀 관계식은 T(n) = T(n/3)이다.

ⓑ 시간 복잡도는 O(n)이다.

④ B항은 하위 문제를 해결 한 후 상위 문제로 결합하는 과정에 소요되는 시간 복잡도이다.
㉠ 상위 문제의 1/2 사이즈인 2개의 하위 문제를 재귀적으로 호출하며, 각 재귀 호출에서 n만큼의 추가적인 시간 복잡도가 소요된다.
| function scissor(array) | |
| n = length(array) | |
| if n > 1 then | |
| scissor(n/2) | |
| scissor(n/2) | |
| for i = 0 to n - 1 do | |
| i = i + 1 | |
| end for | |
| end if | |
| end function |
ⓐ 재귀 관계식은 T(n) = 2T(n/2)+O(n)이다.
㉡ 상위 문제의 1/2 사이즈인 2개의 하위 문제를 재귀적으로 호출하며, 각 재귀 호출에서 n만큼의 추가적인 시간 복잡도가 소요된다.
| function scissor(array) | |
| n = length(array) | |
| if n > 1 then | |
| scissor(n/2) | |
| scissor(n/2) | |
| for i = 0 to n - 1 do | |
| for j = 0 to n - 1 do | |
| j = j + 1 | |
| end for | |
| i = i + 1 | |
| end for | |
| end if | |
| end function |
ⓐ 재귀 관계식은 T(n) = 2T(n/2)+O(n^2)이다.
㉢ 상위 문제의 1/2 사이즈인 2개의 하위 문제를 재귀적으로 호출하며, 각 재귀 호출에서 log n만큼의 추가적인 시간 복잡도가 소요된다.
| function scissor(array) | |
| n = length(array) | |
| if n > 1 then | |
| scissor(n/2) | |
| scissor(n/2) | |
| for i = 0 to n - 1 do | |
| i = i * 2 | |
| end for | |
| end if | |
| end function |
ⓐ 재귀 관계식은 T(n) = 2T(n/2)+O(log n)이다.
③ 마스터 정리를 이용하면 복잡한 재귀식을 매우 쉽게 해결할 수 있다.
㉠ 마스터 정리를 사용할 수 있는 경우의 수는 크게 세 가지이다.
ⓐ A항의 시간 복잡도가 B항의 시간 복잡도보다 클 때
ⓑ A항의 시간 복잡도가 B항의 시간 복잡도보다 작을 때
ⓒ A항의 시간 복잡도와 B항의 시간 복잡도가 유사할 때
④ A항의 시간 복잡도는 n^logb(a)로 결정할 수 있다.
㉠ B항을 생각하지 않고 A항의 시간 복잡도를 구해보자.
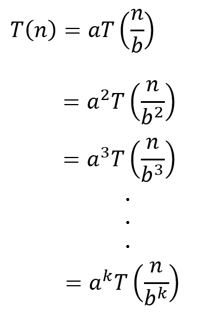


⑤ 따라서 ③번의 내용은 다음과 같이 정리될 수 있다.
㉠ A항의 시간 복잡도가 B항의 사간복잡도보다 작다면, 어떤 상수 ε>0에 대해서 f(n)은 O(n^logb(a-ε))에 속한다고 할 수 있으므로, T(n)의 시간 복잡도는 Θ(n^logb(a))가 된다.
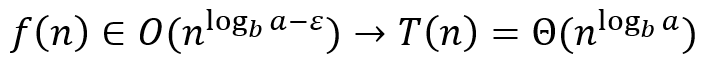
㉡ A항의 시간 복잡도가 B항의 시간복잡도보다 크다면, 어떤 상수 ε>0에 대해서 f(n)은 O(n^logb(a+ε))에 속한다고 할 수 있으므로, T(n)의 시간 복잡도는 Θ(n^logb(a))가 된다.

㉢ A항의 시간 복잡도와 B항의 시간 복잡도와 비슷하다면 Θ(n^logb(a)log(n))이 된다. 증명은 생략한다.
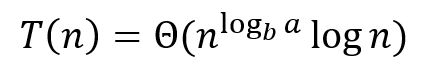
⑥ 다음 예시를 보자. n^(logb(a)) = h(n)이라고 하자.
㉠
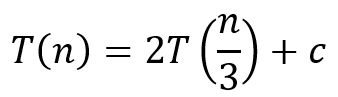
ⓐ a = 2, b = 3이므로, h(n) = n^log3(2)이며, f(n) = c 다.
ⓑ n>N에 대하여 T(n) <= O(n^log3(2)) 이다.
ⓒ 따라서 T(n)의 시간복잡도는 Θ(n^log3(2))이다.
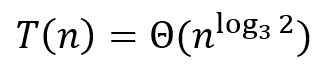
㉡
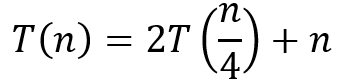
ⓐ a = 2, b = 4이므로, h(n) = n^log4(2)이며, f(n) = O(n)이다.
ⓑ n>N에 대하여 T(n) <= O(n^log4(2)) 이다.
ⓒ 따라서 T(n)의 시간복잡도는 Θ(n)이다.
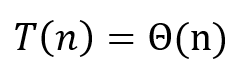
㉢
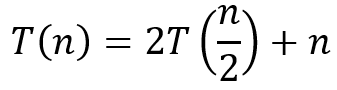
ⓐ a = 2, b = 2이므로, h(n) = n^(log2(2)) = n이며, f(n) = n이다.
ⓑ h(n) = f(n) = n이다.
ⓒ 따라서 T(n)의 시간복잡도는 Θ(nlogn)이다.
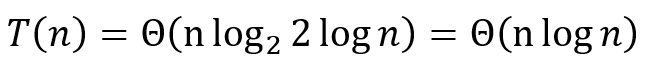
⑦ 마스터 정리의 제약 조건 때문에 모든 재귀 관계식을 풀 수 있는 것은 아니다.
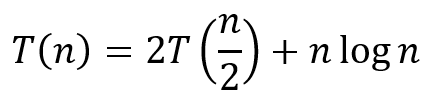
㉠ 어떠한 상수 c < 1에 대해서 af(n/b) <=cf(n)가 성립해야 한다
ⓐ a = 2, b = 2이므로, h(n) = n이며, f(n) = nlog(n)이다. n이 커짐에 따라 n과 nlog(n)은 n에 수렴하게 된다.
ⓑ 공식에 따르면 nlog(n)이 나와야 한다. 그렇지만, 해당 함수의 시간 복잡도는 n^2* log(n)이다.
ⓒ 어떤 c<1에 대해서 af(n/b)<=cf(n)를 만족하는 c가 존재해야 한다.
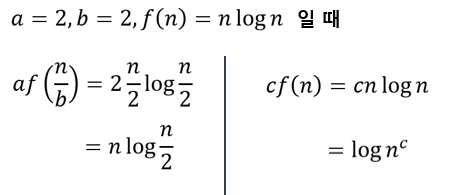

ⓓ 해당 문제는 일반 마스터 정리(generalized master theorem)를 사용해 시간 복잡도를 구할 수 있다.
일반 마스터 정리(Generalized Master theorem)
※ 이 글은 chatGPT를 기반으로 작성한 글입니다. ① 일반 마스터 정리(generalized master theorem)는 고급 마스터 정리(advanced master theorem)와 확장 마스터 정리(extended master theorem)으로도 불린다. ㉠ 일반
hemahero.tistory.com
'All about Data Structure & Algorithm > 심화' 카테고리의 다른 글
| 홀짝 정렬(Odd-Even sort) (0) | 2023.03.31 |
|---|---|
| 향상된 퀵 정렬 (0) | 2023.03.24 |
| 셸 정렬(Shell Sort) (0) | 2023.03.24 |
| 분할 정복(Divide and conquer) (2) | 2023.03.15 |
| 일반 마스터 정리(Generalized Master theorem) (0) | 2023.03.15 |


